In 2021 an unconventional pair of collaborators embarked on a bold experiment. For two years Steven Rayan, a mathematician and mathematical physicist, and Jeff Presslaff, a freelance composer, pianist and trombonist, prepared to answer one big question: Could they translate a mathematical physics research paper directly into music? Moreover, would their musical creation sound good?
In September Rayan and Presslaff released their brainchild, “Math + Jazz: Sounds from a Quantum Future.” Exactly two years to the date that Rayan, a researcher at the University of Saskatchewan, and Presslaff, who’s based in Winnipeg, Canada, first connected over e-mail, they gathered a 15-piece “hyperbolic band” of musicians to perform the five-section concert at the University of Saskatchewan. Each section corresponded to a portion of Rayan’s research article.
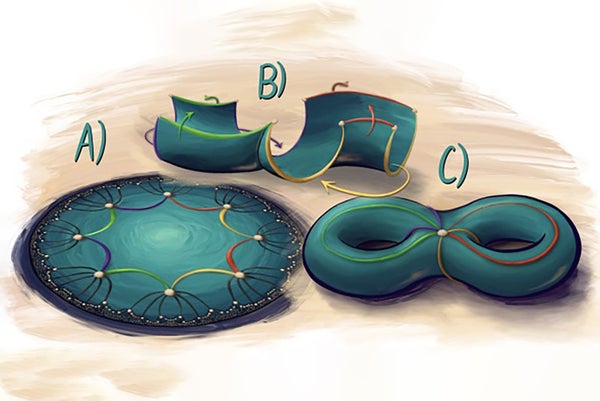
Part musical performance and part lecture, the concert was played to “a packed house,” Rayan says. The lecture portion dissected the paper’s scientific concepts and illustrated how those ideas were transmogrified into music. Some of the illustrations were literal: the slideshow featured hyperbolic art created by Elliot Kienzle.
Pulling off the concert was no easy feat. Because many of the musicians weren’t local, the band hadn’t rehearsed the music together in person until the night before the concert, Rayan notes.
Hyperbolic Band Theory
The music was based on Rayan’s 2021 Science Advances article “Hyperbolic band theory,” which he wrote with Joseph Maciejko of the University of Alberta. Their objective was to explore whether band theory—which researchers use to consider the energy levels of materials and the atoms that they’re made of—could be reformulated to explain hyperbolic materials, which have irregular, warped arrangements.
In band theory a material’s energy levels are thought of as being contained in sheetlike bands hovering above the materials they belong to. These shadowy bands represent the material’s quantum properties, and interactions between these bands have consequences for the material’s behavior.
Rayan and Maciejko succeeded in discovering a band theory that works in the wonky world of hyperbolic geometry, a strange geometrical realm that breaks Euclid’s “parallel postulate.” Also called Euclid’s fifth postulate, this rule tells us the following: Suppose you’re given a line. For any point that isn’t on that line, there will be only one line that both goes through that point and is parallel to the original line. In hyperbolic land, a minimum of two lines will go through the point while also being parallel to the given line.
The research “is a whole new approach to designing materials—especially quantum materials—by re-engineering their geometry from the inside out,” Rayan says. The approach involves altering the material’s band structure to create the desired changes in the material’s properties. “They can take on unusual, exotic geometries,” he says.
This might look like, for instance, covering a curved surface by tiling it with octagons so that there aren’t any gaps between the shapes, which are nonoverlapping. To human eyes, the edges of these octagons appear curved, and the shapes look like they are different sizes, Rayan notes. But “if you had a different kind of eye that sees the world in a hyperbolic way—maybe insectlike compound eyes—[the octagons] might all look the same to you,” he says.
The work received a lot of attention from other researchers. “I’m very impressed by the connection between material science and algebraic geometry which was unearthed by the authors of this paper,” says Michael Groechenig, a mathematician at the University of Toronto, who wasn’t involved with the article.
Rayan is excited to apply his findings to studying unusual materials with the potential for “disruptive applications,” such as in quantum computing. “It’s rather delightful to see someone exhibit an important application of these methods of such a concrete nature,” Groechenig says. The paper is “an invitation for us pure math folks to leave our comfort zone a little and to explore hitherto uncharted territory,” he adds.
Translating to Music
Creating a mathematical concert is its own kind of disruptive application of the research. “I didn’t want [the music] to be impressionistic,” Presslaff says. “I wanted it to be really true to mathematics.... I’ve just seen too many cross-disciplinarity projects that just strike me as superficial. The science side might be rigorous, and the art side is very not rigorous."
Rayan agreed with that goal. “I had a commitment to not just producing music that was somehow loosely inspired by the math and the science but rather somehow retelling the mathematics word for word, equation for equation, in a musical form,” he says.
But embracing that challenge also required that both experts leave their comfort zones and learn concepts from each other’s areas of expertise. Presslaff immersed himself in topics from linear algebra and topology that helped illuminate the inner workings of the research paper. Rayan dove into “trying to understand, as much as possible, the advanced musical ideas [Presslaff] brought to the table.”
The pair exchanged ideas for approximately 18 months before Presslaff even began writing the music. “It’s amazing that I never met Jeff in person until the day before the performance on September 20,” Rayan says. “It was all on Zoom because of the pandemic and because of distance. It was a fascinating way of working—that we could accomplish this even through purely virtual means.”
Double Fugues and Infinite Shapes
It’s tricky to pinpoint whether Rayan and Presslaff met their grand objective: to convert the main ideas from Rayan’s paper directly into jazz music. Unlike in mathematics research, there is no “proof” that they accomplished their goals. Still, the duo is pleased with their result. “Getting it done was just never a certain thing until even, say, six weeks before the performance,” Rayan says.
Hyperbolic Band performer Shah Sadikov, a Baltimore-based violist, says a highlight of the concert was when Presslaff used a double fugue, a musical technique that’s “very difficult to implement,” to represent the process of building an “infinite shape,” Sadikov says. Mathematically, that meant creating an object with “no beginning, no end,” Sadikov says. Musically, creating a double fugue involves making “one idea the foundation of the musical piece and then you take the exact same idea [and] you place it a bit later on top of it,” and so on, he says. “You create these layers of ideas. And then you can use counter ideas to that, either taking the same musical idea [and] putting it backwards or upwards,” he notes.
For Rayan, a highlight was hearing Presslaff’s musical take on “the so-called particle-wave duality or the position-momentum duality in hyperbolic band theory.” In that context, momentums can take on more dimensions than positions can. “We wanted to capture in the music the jump from, say, two dimensions to four dimensions in the simplest of these materials, which are based on octagonal hyperbolic lattices,” Rayan says.
“Hearing [Presslaff’s] attempts at introducing extra voices in the music that capture the extra degrees of freedom, the sudden jump to two extra dimensions, was a moving experience for me,” Rayan says. “I loved watching the audience try to hear those extra voices after [his] explanation of them.”
The concert included one other artistic element: Kienzle’s hand-drawn illustrations. Now a graduate student at the University of California, Berkeley, Kienzle created the mathematical art for a related research project that he and Rayan worked on while he was an undergraduate student at the University of Maryland, College Park. “This was an attempt to tell the story through a visual lens,” Rayan says. In the concert those illustrations helped enhance the musical and verbal explanations of the math and science.
Rayan sees reinterpreting this work through musical and artistic lenses as a way of bringing it full circle. Much of the mathematical and scientific concepts featured in his papers borrow ideas from the world of art. For instance, “hyperbolic tilings are very reminiscent of” Dutch graphic artist M. C. Escher’s iconic woodcuts, he notes. Rayan plans to continue exploring new ways of fusing mathematical and artistic perspectives to “give back to art” while also sprouting new insights for his research.